Langevin Equation

We are going to stochastically solve the Langevin Equation.

We take the Langevin equation. There is a stochastic force in there which is Gaussian in nature.

We will (1) use Euler’s method to generate a realization but for that we first need (2) a sampled Gaussian distribution.

Consult Gerd Ropke’s text on non-equilibrium thermodynamics.

Sampling a Gaussian

Manually (Box-Fuller method)

Let’s try the Box-Fuller method.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

def SampleGaussian(num = 1000):

    u = np.random.rand(num)
    u1 = u[:int(num/2)]
    u2 = u[int(num/2):]

    z0 = np.sqrt(-2*np.log(u1)) * np.cos(2 * np.pi* u1)
    z1 = np.sqrt(-2*np.log(u1)) * np.sin(2 * np.pi* u2)
    z = np.concatenate((z0,z1))
    return z

plt.hist(SampleGaussian(), bins = 10)

(array([  8.,  20., 195., 196., 301., 119.,  72.,  52.,  29.,   8.]),
 array([-2.71806518, -2.09685307, -1.47564096, -0.85442884, -0.23321673,
         0.38799538,  1.0092075 ,  1.63041961,  2.25163173,  2.87284384,
         3.49405595]),
 <BarContainer object of 10 artists>)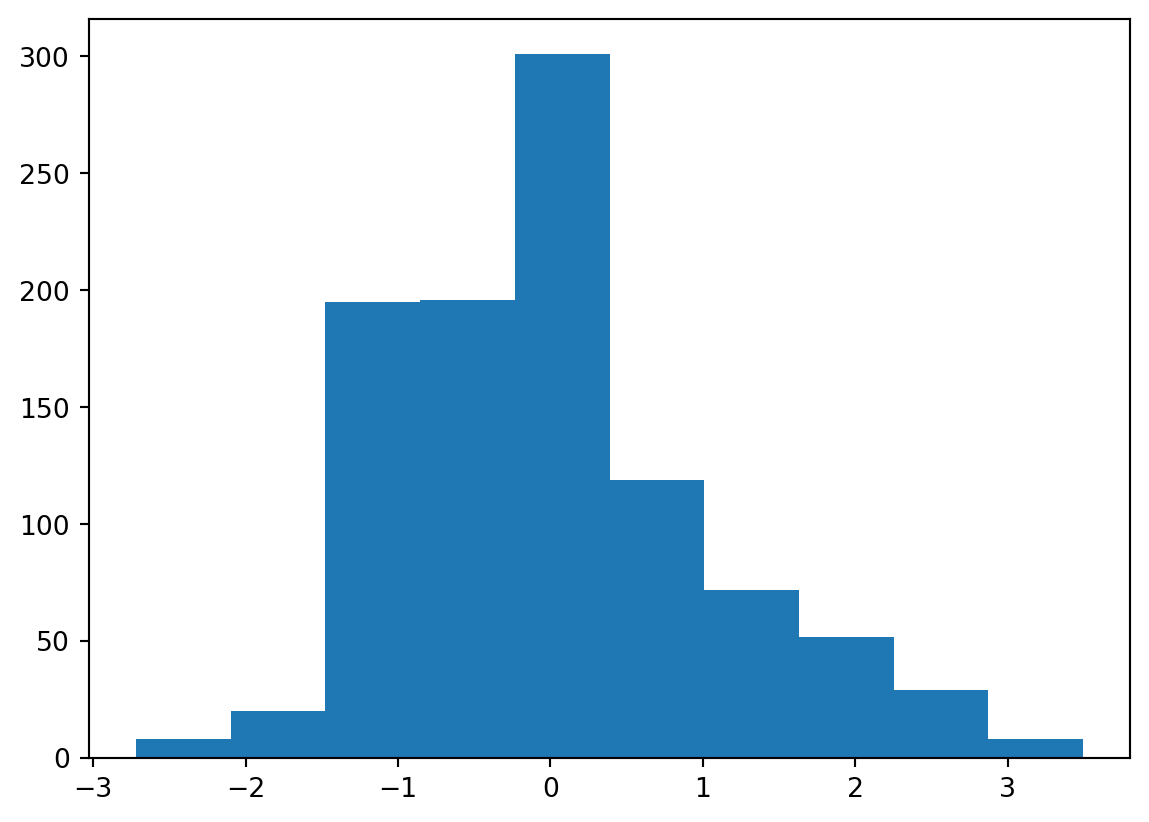

Automatic (use some library)

Numerical solution of the Langevin equation

Use the Euler method

\(v_k^{(m)} = v_{k-1}^{(m)} + h (-\gamma v_{k-1}^{(m)} + r_{k-1}^{m})\)

$M = 1000 (Number of realizations), $ $N = 24000 time steps, $ $h = 0.025, $ \(t_N - t_0 = 600 s,\) \(\gamma = 5; D = 1\)

Solve it directly

• For one realization: Create N random variables.

def eulerlangevin(vk_1, rk_1, h, gamma ):
    return vk_1 + h * (-gamma * vk_1 + rk_1)

def langevinrealizations(h = 0.025, samples = 100, realizations = 10, v0 = 1, gamma = 5, D = 1):
    """
    Create multiple langevin realizations
    Arguments:
        v0 = Initial velocity
        h = time step
        gamma = friction
        D = Diffusion

        time (not passed but total simulation time = h*samples)

    """

    time = np.linspace(0,h*samples, samples)

    allvk = np.empty((realizations, samples))
    allgaussians = np.empty((realizations, samples))

    for m in range(realizations):
        gaussianrv = SampleGaussian(samples)
        vk = np.array([])
        for i in range(len(gaussianrv)):
            if i == 0:
                vk = np.array([v0]) #np.append(vk, eulerlangevin(v0, gaussianrv[0], h, gamma))
            else:
                vk = np.append(vk, eulerlangevin(vk[i-1], gaussianrv[i-1], h, gamma))

        allvk[m] = vk
        allgaussians[m] = gaussianrv

    return time, allvk, allgaussians
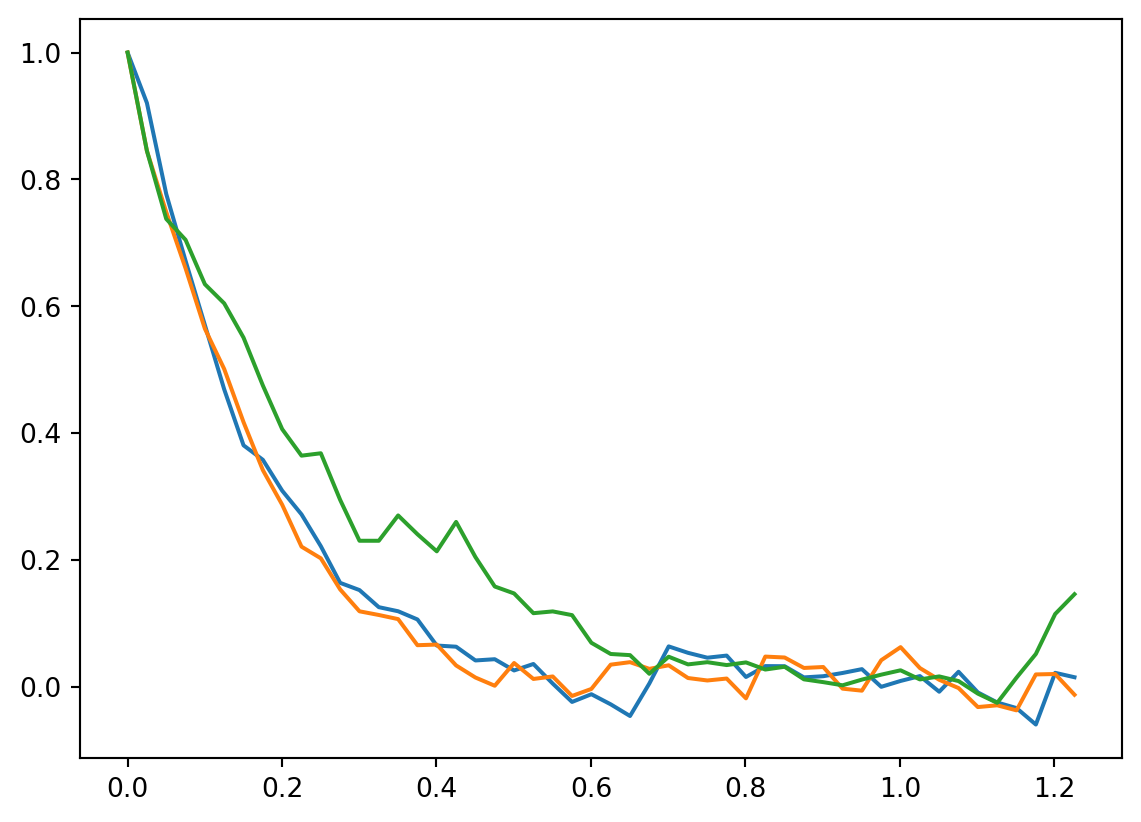
time, allvk, allgaussians = langevinrealizations(samples = 1000, h = 0.025, gamma = 5, D = 1, realizations = 10)

We plot some realizations.

n = 50
plt.plot(time[:n], allvk[0][:n])
plt.plot(time[:n], allvk[1][:n])
plt.plot(time[:n], allvk[2][:n])